Romberg
四月 22, 2016
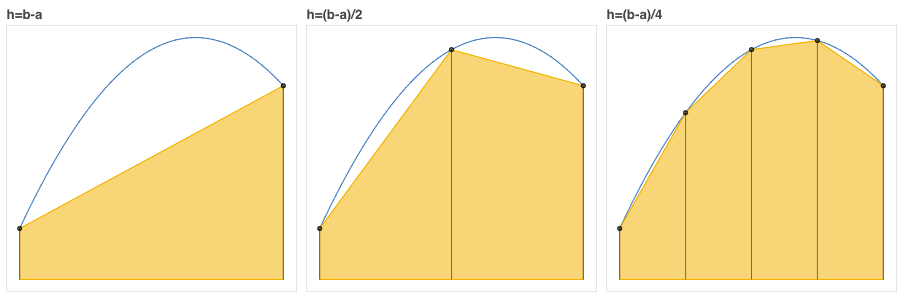
龙贝格数值积分算法,以复化梯形公式为基础,用查理森加速外推方法把低精度的积分线性组合成高精度的积分,减少了运算量。
下面是matlab代码
1 | function I=Romberginterg(fun,a,b,npanel,tol,flag) |
1 | function I=Trapezoidinteg(fun,a,b,npanel) |
查看评论

龙贝格数值积分算法,以复化梯形公式为基础,用查理森加速外推方法把低精度的积分线性组合成高精度的积分,减少了运算量。
下面是matlab代码
1 | function I=Romberginterg(fun,a,b,npanel,tol,flag) |
1 | function I=Trapezoidinteg(fun,a,b,npanel) |